미분은 무엇일까?
딥러닝 공부를 하니 미분이 나타났다.
대학 때 미적분학 A+ 받은 기억을 더듬어 다시 정리해 본다.
미분이 쉽지는 않다.
그 이유는 바로 개념을 정확히 이해하지 못했기 때문이다.
그저 공식만 외우고 문제에 적용해 풀기만 해서 그래 보였다.
그렇다면 미분은 무엇일까?
함수 그래프의 특정 한 점에서 접선한 부분의 기울기, 미분 계수, 를 구하는 방법이 미분이다.
참 어려운 표현이다.
우선적으로,
미분을 쉽게 이해하기 위해 용어 하나씩 정리해 보자.
Δx(델타 x)는 무엇인가?
미분 공부를 하면 특이한 기호들이 많다.
변수 x 앞에 Δx 이런 기호가 붙어 있다.
어떻게 사용하는지 예를 들어 보자.
오늘 아침 9시 수도 계량기 지침은 3301이었다.
한 시간 뒤 10시에 보니 3304로 3만큼 사용했다.
시간당 3의 사용량(3304-3301)을 보였다.
여기서 초기값 3301가 x이고 x의 증가한 값(물 사용량) 3이 Δx(변화량)이 된다.

관리비 고지서에 한 달 수도사용량도 당월지침 - 전월지침으로 계산된다.
이렇게 수도 사용량을 가지고 요금이 정해진다.
Δx는 x 값의 증감된 값, 변화량을 의미한다.
Δy/ Δx는 평균 변화율이다.
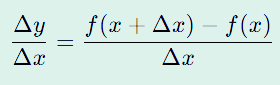
우와~ 이건 또 어떻게 이해해야 하나?
Δx는 얼마나 변했는지 나타내는 변화량인 건 알겠는데 Δy/ Δx는 뭘까?
위 식을 보면 평균 변화율이라고 하는데 다음과 같이 이해하면 된다.
위 식의 분자 부분을 보면 Δy = f(x + Δx) - f(x)로 되어 있다.
오른쪽 식을 설명하면,
함수 f()에 시작값 x에 변화량 Δx를 더해서 넣은 결괏값에 f()에 시작값 x를 넣은 결괏값을 뺀다.
수도 계량기 값을 넣어보면

결과는 Δy/ Δx = 1이다.
Δx로 나누었기 때문에 평균값이 된다.
그래서 위 식을 함수 y = x의 평균 변화율이라고 하고 그 값은 1이고 기울기를 의미한다.
정리.
평균 변화율은 x값에 의해 y가 얼마나 변했나.
평균 변화율은 함수 그래프의 한 점에 대한 기울기(경사)다.
미분을 배우려면 평균 변화율은 반드시 알아야 한다.
y = f(x), 함수 y = x에서 x값의 변화에 따라 y값도 변한다.
평균 변화율은 함수의 기울기로 이해해도 된다.
도함수란?

위 함수의 그래프는 U자형으로 그려진다.
x의 위치마다 y의 값이 달라지고 그 점의 접선 기울기도 다르다.
미분으로 이 값을 구할 수 있다.
f(x)를 미분하면 새로운 함수를 만들게 된다.
그 함수는 f'(x)가 되고 도함수라고 읽는다.
도함수는 각 점 x의 순간 변화율인 접선 기울기를 구하기 위한 용도다.
이는 다음과 같다.

변화율에서는 Δx 기호를 사용했다.
dx는 또 무슨 의미일까?
d는 differentiation의 약자로 미분입니다.
차로 도로를 달리면 순간순간 속도가 다르다.
그 속도를 계기판으로 실시간 확인한다.
점으로 콕 찍어 특정 시간대 속도(기울기, 변화량)를 구하는 것이 미분이다.
Δx처럼 큰 범위의 값이 아닌 그냥 거의 0과 가까운 값을 구하는 것이다.
위 함수는 그래프가 U 형태라고 했다.
기울기는 x 값에 따라 다를 것이다.
특정 위치의 기울기(미분값)를 구하는 함수가 도함수다.
도함수는 원래 함수를 미분해서 만든다.
정리.
도함수를 표시하는 방법은 다양하다.
1. 라그랑주 표기법(가장 흔히 사용)
- 함수 : f(x)
- 도함수 : f′(x)
2. 라이프니츠 표기법
- 함수 : y=f(x)
- 도함수 : dy/dx (분수형태)
f'(x)가 x의 변화율(기울기)를 나타내는 도함수라고 했는데 위 식처럼 dy/dx도 도함수를 의미한다.
분수처럼 생겼지만 dy/dx도 평균 변화율과 같은 의미다.
y를 x로 나누는 분수가 아니다.
x가 변할 때마다 y는 얼마나 변하나?라는 의미다.
위 함수의 도함수는 2x가 나왔다.
즉, x 값이 바뀔 때 y는 2x만큼 변한다는 의미다.
도함수 구하는 예제

이론만 보면 정확히 이해가 어려울 수 있다.
실제 예를 들어봤다.
먼저 위 첫 번째 라인에서 함수를 선언했다.
y = x2 함수를 미분해서 도함수로 만드는 과정이 세 번째 라인이다.
f(x)의 도함수는 f'(x) = 2x가 된다.
x = 1일 때 미분값은 f'(1) = 2×1 = 2가 된다.
극한식으로 미분 풀어보기

극한식 (lim)까지 등장했다.
사실 어렵지 않다.
h → 0 은 h(x의 변화량)가 0에 가까워진다는 의미다.
식은 평균 변화량 식을 극한으로 보낸다는 의미다.
즉 평균 변화량이 미분과 관계가 있다는 것이 여기서 보인다.
위 식을 값을 넣어 한 번 풀어보자.

y = x2 함수를 기준으로 x = 2를 대입해 본다.
f'(x) = 2x고 2를 대입하면 다음과 같이 식을 푼다.
1. 쉽게 구하기
도함수 f'(x) = 2x에 2를 대입하면 4. 끝.
2. 극한식으로 구하기
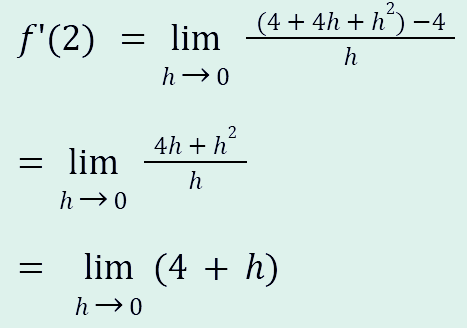
h가 0으로 수렴한다.
그래서 결과는 h가 0에 근접하기에 4에 가까워져 4가 나온다.
미분연산자?

위 식은 도함수인지 이제 안다.
그런데 비슷한 식이 있다.

위 식은 위에 y가 없다.
이 구조는 x에 대해 미분하라는 의미다.
분수도 아니고 계산식도 아닌 미분하라는 연산자로 보면 된다.
마치 + 는 더해라~와 같다.
마무리
미분을 처음 보면 이상한 기호들이 많다.
기존에 알고 있던 분수 형태를 그대로 적용하면 이해가 안 된다.
미분은 미분만의 특별한 형태가 있고 위에 쉽게 설명해 봤다.
여기서 끝은 아니다.
미분에 대한 이야기는 더 있다.
'Education > Math(수학)' 카테고리의 다른 글
| [에세이]1학기에 망한 수학 성적, 수학 근육 만드는 방법으로 올리기. 고1 수학 (0) | 2024.10.08 |
|---|---|
| [HOW]고등학교 수학 1등급 문제 푸는 방법, 수학 공부 잘하는 방법 (0) | 2020.11.09 |
| [수학_중1_수와 연산]소인수분해 3탄 (쉽게 설명하는 중학교 수학) (0) | 2019.04.28 |
| [수학_중1_수와 연산]소인수분해 2탄 (쉽게 설명하는 중학교 수학) (0) | 2019.04.14 |
| [수학_중1_수와 연산]소인수분해 1탄 (쉽게 설명하는 중학교 수학) (0) | 2019.04.06 |