신기한 연구소

딥러닝(Deeplearning)에서 손실 함수란?

딥러닝 스터디 중 손실 함수(loss function)를 알게 되었다.

머신러닝, 딥러닝에서 해당 모델의 성능을 평가할 사용하는 함수다.

모델이 예측, 인식한 값과 실제 값과의 오차를 알려준다.

손실 함수는 회귀와 분류 문제로 구분되어 있다.

용어도 어렵고 계산식도 한참을 봤다.

인공지능 학습이 쉽지 않을 거라 생각은 하고 있었다.

최대한 쉽게 이해하고 싶어 꼼꼼히 정리해 봤다.

손으로 숫자 5를 써서 딥러닝 학습을 통해 인식하고자 한다.

숫자 5를 썼지만 학습 결과 5일 확률이 0.3 정도 나왔다 가정하자.

1을 기준으로 무려 0.7을 잘못 인식했다는 결과다.

숫자 5인데도 손으로 쓴 글씨라 0.3 정도만 인식했다는 의미다.

무려 0.7을 잘못 인식했다고 알려줘야 한다.

인식률을 높여 숫자 5로 인식하게 알려줘야 한다.

바로 손실 함수가 그 역할을 한다.

즉, '얼마나 잘못 예측했나'를 수치로 보여주는 함수가 손실 함수다.

회귀 문제

과거 거래량, 과거 주가, 경제 전망 등을 활용해서 앞으로의 주가를 예측한다.

예측하는 주가는 입력값에 따라 결정된다.

입력값의 종류와 값 범위에 따라 결괏값이 결정된다는 의미다.

회귀는 결괏값이 연속적이라는 특징이 있다.

주가가 0 또는 1처럼 둘 중 하나값이 아니다.

이런 경우를 분류문제라고 한다. 0 또는 1.

회귀는 입력값이 따라 연속적인 금액값 중 하나가 종속된다.

이번 포스팅에서는 회귀 문제에 대한 손실 함수를 먼저 확인해 보자.

사실 용어만 봐서는 감이 안 잡힌다.

손실 함수 중 회귀 문제는 평균 제곱 오차(Mean Squared Error, MSE)와 오차 제곱 합(Sum of Squared Errors, SSE).

우선 이 2개의 함수를 확인해 보겠다.

평균 제곱 오차(Mean Squared Error, MSE)

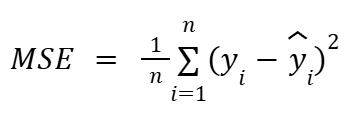
우와~ 어려운 식이 나타났다.

∑ (이하 시그마)를 처음 본다면 당황스러울 수 있다.

어렵지 않다.

시그마는 우측 식을 i=1부터 n까지 순서대로 대입한 값을 전부 더한다는 의미다.

간략하고 쉬운 식을 보자.

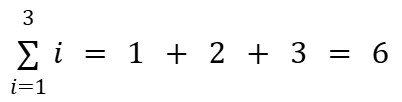
시그마 옆 i에 1부터 3까지 입력한다.

1 + 2 + 3으로 식이 만들어지고 결과는 6이 된다.

평균 제곱 오차(Mean Squared Error, MSE)의 경우는

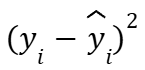
다음 식을 i=1부터 n번째까지 값들을 위 예제 식처럼 쭈욱 더한다는 의미다.

그리고 1/n으로 나누는 의미다. 0.5를 곱해도 된다.

식에 대한 설명을 했다.

이제 딥러닝에서 평균 제곱 오차(Mean Squared Error, MSE)를 사용하는 예를 들어보자.

3번 라인은 mean_squard_error함수로 평균 제곱 오차(Mean Squared Error, MSE)를 구현했다.

np.mean이 수식의 복잡한 평균을 쉽게 구해준다.

t는 true value로 6번 라인 index 4번째가 1이다.

y는 추측값을 가정해서 만들어 봤고 8번 라인 index 4번째가 0.7로 높은 확률이 나왔다.

함수를 실행하면 결과는 0.011500000000000003가 나온다.

정말 작은 수이다.

만약 true value는 그대로인데 17번 라인을 보면 index 4번째가 0.1로 낮은 확률이 나왔다.

그 결과 함수를 실행하면 결과는 0.1315으로 0.7로 나온 경우보다 높은 값이 나왔다.

결론은 결과가 낮을수록 오차가 적다는 의미로 볼 수 있다.

결괏값을 보고 오차를 조정하면 된다.

오차 제곱 합(Sum of Squared Errors, SSE)

(실제 값 - 예측 값)의 제곱을 2로 나눈 식이다.

약간 변형된 식을 보기도 한다.

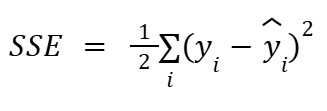
이 식은 시그마의 인수값이 다르다.

위 쪽에 인수값 n이 없고 아래 i만 있다.

i=1부터 n까지도 아니고 달랑 i 하나면 값을 하나만 받는다는 의미일까?

numpy.array를 실제값과 예측값에 할당하면 비록 배열 하나지만 내부의 많은 값을 활용할 수 있다.

예제 소스를 보자.

4번 라인의 식을 보면 np.sum을 사용했다.

합계 구하고 반으로 나눴다.

식은 심플하다.

7번 라인 t는 index 4번째 값이 1이다.

9번 라인 y는 index 4번째 값이 0.7로 높은 확률이다.

결과는 0.057500000000000016로 아주 작은 값이 나왔다.

그렇다면 오차가 크면 어떨까?

18번 라인 y는 index 2번째 값이 0.7이고 매칭되는 index 4는 0.1로 낮은 확률이다.

결과는 0.6575로 0.7보다는 꽤 큰 값이 나왔다.

마찬가지로 결과 값이 0에 가까워질수록 오차가 없어진다는 의미고,

결과 값이 0보다 커질수록 오차도 커진다는 의미다.

제곱이라 오차가 커질수록 더 큰 차이가 나타난다.

정리.

손실 함수 중 회귀 문제를 다루는 함수 2 종류를 확인했다.

평균 제곱 오차(Mean Squared Error, MSE)와 오차 제곱 합(Sum of Squared Errors, SSE) 두 함수다.

손실 함수로 출력 값으로 정확도와 오차를 확인할 수 있다.

그 값을 활용해 신경망 성능을 향상할 수 있다.

오차를 줄여서 정답에 가까워져라~~~

지금까지 손실 함수 중 회귀 문제에 대해 정리해 봤다.

잘못된 정보는 댓글 바란다.

다차원 배열(행렬)은 딥러닝에서 신경망 구현시 필수로 알아야 하는 부분이다.

배열(Array)이나 행렬은 프로그래밍 언어나 수학을 배울 때 들어봤을 것이다.

딥러닝에서 신경망에도 다차원 배열이 꼭 필요하다고 한다.

어렵지 않으니 기본 개념부터 하나씩 같이 살펴보자.

다차원 배열과 행렬

C나 자바 같은 프로그래밍 공부를 했다면 배열(Array)을 배웠을 것이다.

파이썬 딥러닝은 넘파이(Numpy)에서 배열(Array)을 지원한다.

숫자 1부터 5까지 같은 데이터타입(숫자)을 만든다.

2차원 배열은 어떻게 만들까?

1차원 배열과 달리 2차원 배열은 [1,2,3]과 [4,5,6]을 []로 한 번 더 구분했다.

딥러닝 신경망을 구현하려면 배열로 된 행렬의 연산이 필요하다.

위 1차원 2차원 배열을 행렬로 표시하면 아래와 같다.

2차원 배열부터 다차원 배열(행렬)이라 한다.

행렬은 뭘까? 행과 열을 의미한다.

가로로 보는 행이 2줄이다. 1 2와 3 4.

세로도 열이 2줄이다. 1 3과 2 4.

가로는 행 세로는 열이라고 한다.

그래서 행렬이다.

위 행렬은 행이 2개 열이 2개라 2 × 2 행렬이라고 부른다.

행렬 곱셈 하는 방법

딥러닝 신경망에서 다차원 배열(행렬)이 필요하다.

그러기 위해서 행렬의 곱셈을 알아야 한다.

그 이유는 뒤에 나온다.

우선 학교 다닐 때 배운 행렬의 곱에 대해 살펴보자.

2 × 2 행렬 두 개를 곱하는 식이다.

곱하는 방법은 아래와 같다.

1. 첫 번째 행렬의 1행과 두 번째 행렬의 1열을 곱한다.

2. 1 × 5 + 2 × 7 = 19로 1행 1열의 값이 된다.

3. 첫 번째 행렬의 1행과 두 번째 행렬의 2열을 곱한다.

4. 1 × 6 + 2 × 8 = 22로 1행 2열의 값이 된다.

5. 첫 번째 행렬의 2행과 두 번째 행렬의 1열을 곱한다.

6. 3 × 5 + 4 × 7 = 43으로 2행 1열의 값이 된다.

7. 첫 번째 행렬의 2행과 두 번째 행렬의 2열을 곱한다.

8. 3 × 6 + 4 × 8 = 50으로 2행 2열의 값이 된다.

행렬의 곱은 새로운 행렬을 만든다.

직접 계산을 해보자.

눈으로만 보면 실수할 확률이 높다.

행렬의 곱셈, 파이썬 넘파이 (Python, Numpy) 

이제 직접 행렬 곱셈을 코딩해 보자.

numpy를 import 해서 array를 사용해야 된다.

6번 라인을 보면 numpy 함수 dot을 사용하고 있다. (np.dot())

행렬곱을 계산해 주는 기능은 dot 함수로 할 수 있다.

행렬곱을 할 경우 주의할 점이 있다.

모든 행렬을 곱할 수 없다. 조건이 있다.

첫 번째 행렬의 열과 두 번째 행렬의 행은 같은 숫자여야 한다.

2 × 2 행렬 곱하기 2 × 2 행렬인 경우 앞의 열 2와 뒤의 행 2가 같다.

만약 2 × 3 행렬 곱하기 3 × 4 행렬인 경우도 앞의 열 3과 뒤의 행 3이 같다.

2 × 2 행렬 곱하기 3 × 2 행렬인 경우 앞의 열 2와 뒤의 행 3이 다르다. 계산할 수 없다.

하나가 1차원 배열인 경우,

2 × 2 행렬 곱하기 2 배열은 첫 번째 2열과 두 번째 2가 같기에 가능하다.

2 배열 곱하기 3 × 2 행렬은 첫번째가 2이고 두 번째 행렬의 행은 3이라 다르다. 계산할 수 없다.

파이썬 코드로 확인해 보자.

결과는 다음과 같다.

6번 라인은 A1의 행렬로  (4, 3)

7번 라인은 A2의 행렬로 (3, 2)

A1의 열과 A2의 행이 3으로 같다. 그래서 오류 없이 결과가 나온다.

4번 라인을 보면 2 × 2 행렬이다.

6번과 7번 라인을 보면 (4, 3) (2, 2)가 되고 첫번째 열은 3 두 번째 행은 2 다르다.

위 코드를 실행하면 오류가 난다.

2 × 2 행렬 곱하기 2 배열도 코딩해 보자.

첫 번째 열 2와 두 번째 1차원 2 배열과 일치한다. 

잘 실행된다.

이 예제는 1차원 배열과 2차원 행렬의 곱이다. 

첫 번째 1차원 2와 두 번째 2차원 행인 2와 일치해서 잘 된다.

다차원 배열, 행렬과 신경망과의 관계

이전 포스팅에서 신경망의 구조와 퍼셉트론에 대해 알아봤다.

2025.03.21 - [인공지능(AI)/딥러닝(DeepLearning)] - [딥러닝]신경망과 활성화 함수(계단 함수, 시그모이드 함수, ReLU 함수) 계산 방법. 초보용 핵심 정리.

신경망은 입력층, 은닉층 그리고 출력층으로 구성되어 있다.

퍼셉트론을 보면 가중치(w)와 편향( 𝞱)을 활용해 계산 후 출력값을 만든다.

여기서, 다차원 배열(행렬)이 신경망에서 어떻게 활용되는지 궁금해진다.

먼저 신경망과 퍼셉트론의 예를 보자.

입력층, 은닉층, 출력층이 있는 신경망 구조의 예다.

입력값은 x₁, x₂로 1차원 배열로 보자. 

입력층이 가중치(w)와 곱하고 편향을 더하면 은닉층의 a₁, a₂ 값이 나온다.

이 식을 행렬의 곱으로 계산하면 된다.

처음 1차식 2 배열과 가중치 2차식 2 × 2 행렬을 곱한 뒤 편향 b를 더한다는 의미다.

이렇게 그림으로 그리면 입력층 x가 1, 2로 2개이고 가중치 시작 밑이 1과 2만 있어 2개라 계산이 가능하다는 의미다.

만약 가중치 밑 3이 존재한다면 구조 자체가 잘못된 것이라는 의미다.

은닉층 a 가 3개라도 가중치 시작 밑은 1과 2면 된다.

그림으로 간단하게 보자.

x₁의 선은 빨간색이다. x₁에서 출발했게이 w밑이 1로 시작하고 a1로 도착하면 w밑이 1로 끝난다. w₁₁   

x₂의 선은 파란색이다. 만약 a₂로 간다면 x₂에서 시작, a₂로 도착이기에 w₂₂가 된다.

x3가 없는데 x₃에서 출발 a₁에 도착하는 가중치 w₃₁을 초록색으로 표현했다.

?를 보면 x₃ 이 없다. 그래서 행렬 곱이 불가능하다는 의미다.

신경망, 활성화 함수 그리고 행렬곱

다차원 배열(행렬) 곱을 파이썬 넘파이(Python Numpy)로 코드를 작성해 보자.

실제와 유사하게 활성화 함수도 추가했다.

지금까지 공부한 부분을 복습하고 확인하는 과정이라 생각하자.

시작~

import numpy as np

# 활성화 함수 시그모이드
def sigmoid(x):
 return 1 / (1 + np.exp(-x))

# 입력값 x 2개 설정
x = np.array([1.0, 2.0])

# 가중치 w
w = np.array([[0.1, 0.4], [0.2, 0.5]])

# 편향 b
b = np.array([0.1, 0.2])

# 계산해보자.
# 입력값 x와 가중치 w로  dot 함수로 행렬곱 계산 더하기 편향.
a = np.dot(x, w) + b

# 활성화 함수에 a 적용
z = sigmoid(a)

# 결과 출력
print(z)

# 결과 [0.64565631 0.83201839]

직접 코딩해 보자.

위 코드를 직접 복사해서 사용해도 된다. 마지막 라인에 결과도 추가했다.

친절하게 주석도 달았으니 자세히 살펴보면 이해될 것이다.

안되면 댓글에~

지금까지 딥러닝 신경망에서 중요한 역할을 하는 다차원 배열(행렬)의 곱셈에 대해 알아봤다.

이제 우리는 딥러닝 신경망에서 다차원 배열(행렬) 곱셈을 활용할 수 있게 되었다.

열공 열코딩~